Introductory discounts!
Save 20% and more on ChordConverter - valid until 2025/07/20 🔥
Special bundle sale: 25% off on ChordPotion + ChordConverter Plus.
Introductory discounts!
Save 20% and more on ChordConverter - valid until 2025/07/20 🔥
Special bundle sale: 25% off on ChordPotion + ChordConverter Plus.
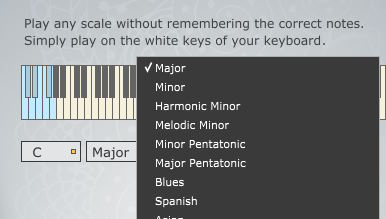
I wrote a MIDI plug-in that contains over 300 scales - also this one here.
Simply pick a scale and play it fluently on your keyboard.
You will always stay on the right notes. Master your melody game in hours instead of years.
Find out more





















